Suppose you have a 16 port device with 8 inputs and 8 outputs. When you perform a UOSM or TOSM calibration on 16 ports and measure, the ZNB(T) will measure all s-parameters. This includes the s-parameters measured with a source at an output port. Measuring these extra s-parameters takes time. For the example above, where you have 8 inputs and 8 outputs, you can cut your testing time in half by eliminating these measurements. The trick is to indicate during calibration that you are only interested in particular s-parameters. This is done by performing multiple one path two port calibrations.

Setting this up is a little tricky. I'll break the explanation into these parts:

• Enabling multiple calibrations
• Performing multiple one path, two port calibrations
• Verifying the time savings
• Saving data
• Simplifying calibration steps

Enable Multiple Calibrations

The first thing you need to do is activate the "multiple calibrations" feature. This allows you to perform and use multiple calibrations simultaneously. These calibrations will become active on a trace-by-trace basis depending on the calibration and measurement. This concept should become clear as we set up the calibration.

To activate this, go to:

Setup (hard key) -> System (tab) -> System Config... (button)

A system configuration window should pop up. On that window, enable the following option:

calibration (tab) -> Multiple Cal in Calibration Wizard (checkbox)

The end result should be:

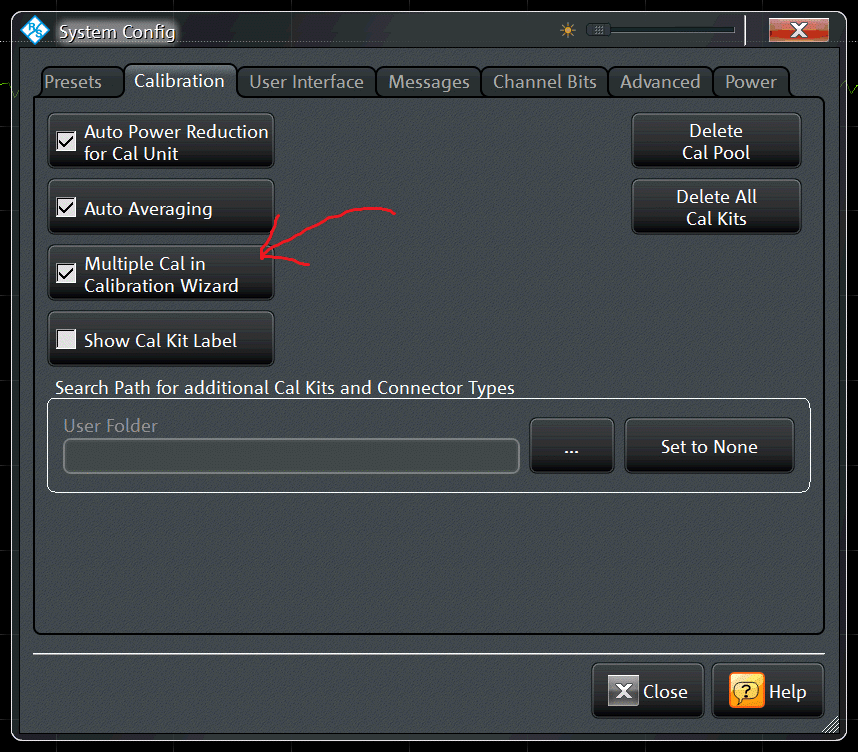
Now when you calibrate you are presented with an extra dialog that lets you define multiple calibrations to perform as a group. We will use this to perform (per the example) 8 one-path two-port calibrations, one for each input port.

Performing Multiple One Path, Two Port Calibrations

To begin, start your automatic calibration as normal:

Cal (hard key) -> Start Cal (tab) -> Start... (Cal Unit) (button)

You should now be presented with this unfamiliar dialog:

This screen allows you to add multiple, independent calibrations to your calibration routine. Click the +Add... button to add the first one-path two-port calibration to the list.

The settings should be as follows:

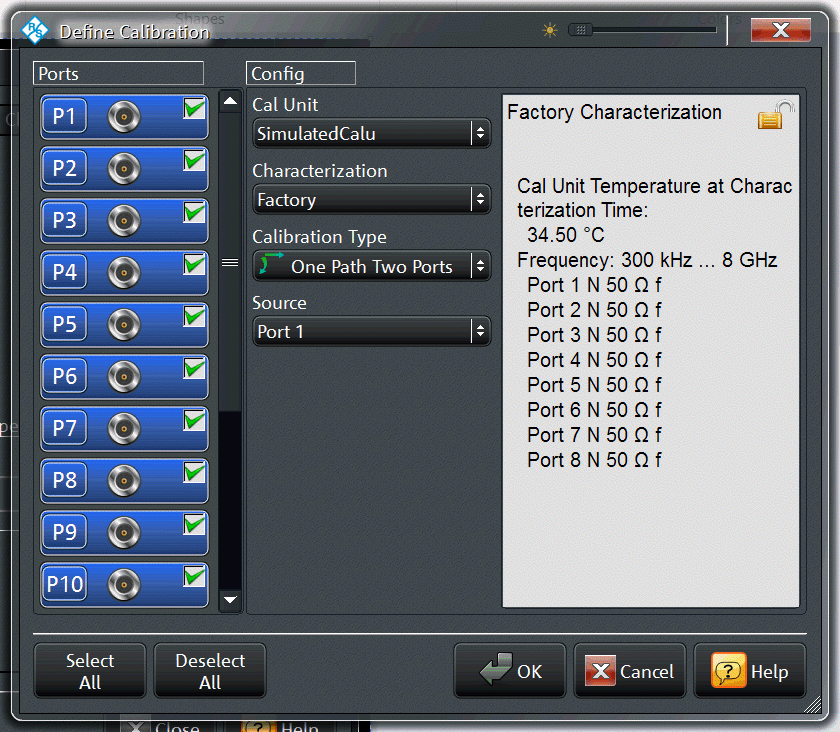
The important parts are:

Setting	Value
Ports	Per your measurement
Calibration type	One Path Two Port
Source	Port 1

For this example, I selected all 16 ports. The source (in this case Port 1) corresponds to the input port that you are calibrating. So, the settings above will calibrate the partial sweep that covers a source at Port 1: S11...S1601.

Repeat this step once for each source port that you are interested in. For our example, the resulting calibration list should look like this:

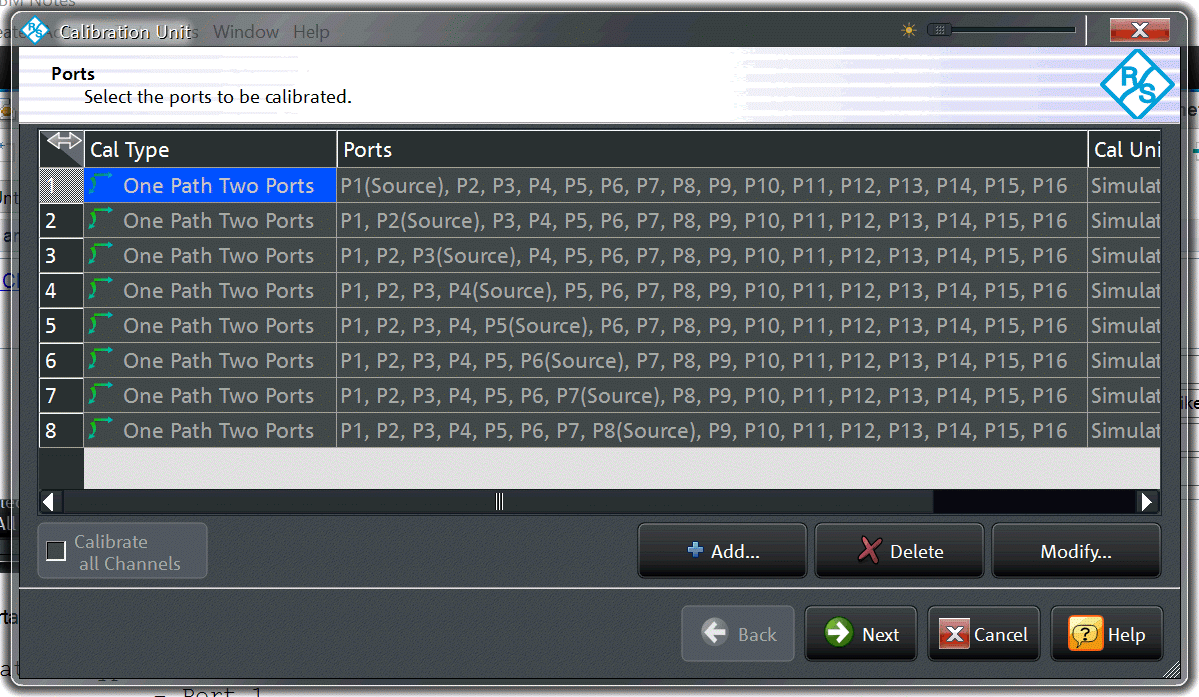
Click next. You should arrive at a screen that allows you to set the cal unit ports used for each calibration. With an 8 port cal unit attached, I get this:

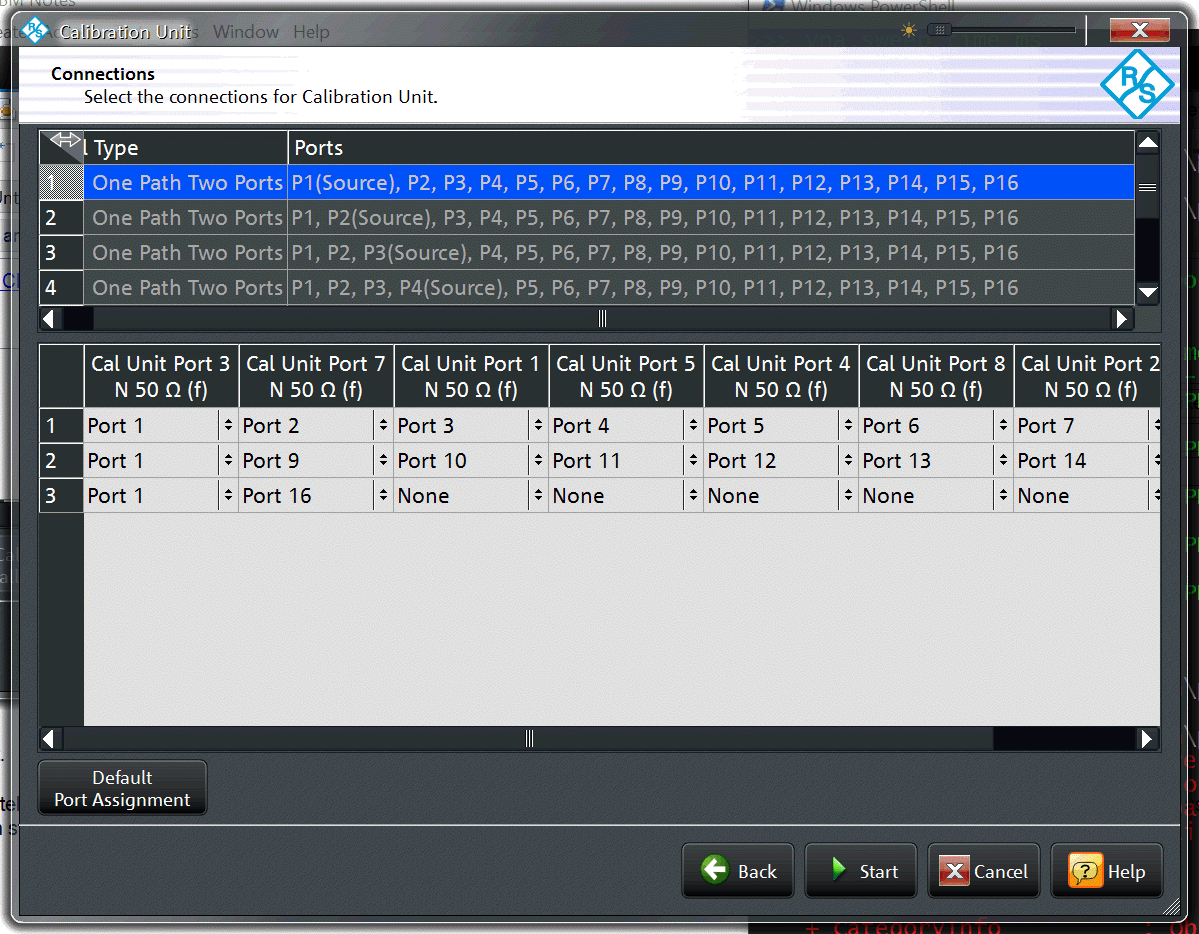
At this point you may have noticed: doing 8 one path two port calibrations generates a lot of calibration steps - for our example there are 24 calibration steps in total (8 calibrations x 3 steps each with an 8 port cal unit => 24 total steps). I have some thoughts on how to simplify this that I'll come back to at the end. For now, we perform the calibration as is.

Verifying the Measurement Time Savings

To verify that this calibration scheme saves time over a single 16-port UOSM or TOSM calibration, I wrote a software application that does the following measurements and records the time that the sweeps take.

1 Partial Sweep:  Traces S11..S1601 
2 Partial Sweeps: Traces above, plus S12..S1602 
3 Partial Sweeps: Traces above, plus S13..S1603 
... 
8 Partial Sweeps: Traces above, plus S18... S1608 

As a sanity check, I started with a preset and uncalibrated VNA. the default settings are:

IF BW  = 10 KHz
points = 201

In an uncalibrated state, the VNA will only perform the measurements necessary for the traces on-screen. Sure enough, my experiments confirm this:

Sweep time vs number of partial sweeps - Uncalibrated

Partial Sweeps	Time (ms)
1	17
2	35
3	52
4	70
5	87
6	105
7	123
8	140
9	158
10	175
11	193
12	211
13	228
14	246
15	263
16	281

Also, as a sanity check, I measured the sweep time for a full 16-port UOSM calibration. Now the VNA will measure all s-parameters regardless of the traces on-screen.

Sweep time vs number of partial sweeps - 16 port UOSM Calibration

Partial Sweeps	Time (ms)
1	281
2	281
3	281
4	281
5	281
6	281
7	281
8	281
9	281
10	281
11	281
12	281
13	281
14	281
15	281
16	281

And finally, the same set of measurements with our 8 separate One Path, Two Port calibrations:

Sweep time vs number of partial sweeps - 8 One Port, Two Path Calibrations

Partial Sweeps	Time (ms)
1	17
2	35
3	52
4	70
5	87
6	105
7	123
8	140
9	158
10	175
11	193
12	211
13	228
14	246
15	263
16	281

As you can see, the VNA is only measuring the s-parameters for the traces on-screen. For an 8 input, 8 output device the measurement time goes down from 281 ms to 140 ms.

In general, the measurement time with multiple one path two port calibrations instead of UOSM or TOSM is approximately:

t = t_uosm * number of input ports / total number of ports

Saving Data

Because we are not measuring the entire s-parameter matrix, we cannot save the data to a touchstone file (S16P). Instead, we can save the complex data for each trace into a CSV file. If you still need a touchstone format file you can create one in post-processing. Beware: to do this you will need to intersperse the measured s-parameters with dummy data as placeholders. Remember not to inadvertently use this dummy data.

Simplifying the Calibration Steps

It seems to me that one path, two port calibration should generate a subset of the same corrections generated in a full TOSM or UOSM calibration. If this is true we should be able to instead perform a UOSM or TOSM calibration, then write a program to read the corrections and create several one port, two path calibrations.

For my example above (16 ports, 8 port cal unit) a full UOSM calibration involves only three steps. These three steps generate corrections for all sources and all S-parameter terms. This would dramatically reduce the number of steps needed.

I will have to explore this when I have time…